Temas de Matematicas Blog de Fin de Semestre M.M

                             INSTITUTO SUPERIOR TECNOLOGICO SUCRE

Nombre: Maicol Moncayo

Curso: Primero A Electromecánica

TEMA: Tablas de verdad

Una tabla de verdad, o tabla de valores de verdades, es una tabla que muestra el valor de verdad de una proposición compuesta, para cada combinación de verdad que se pueda asignar.1

Fue desarrollada por Charles Sanders Peirce por los años 1880, pero el formato más popular es el que introdujo Ludwig Wittgenstein en su Tractatus logico-philosophicus, publicado en 1921.

Definiciones en el cálculo lógico

Para establecer un Sistema formal se establecen las definiciones de los operadores. Las definiciones se harán en función del fin que se pretenda al construir el sistema que haga posible la formalización de argumentos:

- Como razonamientos deductivos lógico-lingüísticos

- Como construcción de un sistema matemático puro

- Como una aplicación lógica en un Circuito de conmutación.

Verdad

El valor verdadero se representa con la letra V; si se emplea notación numérica se expresa con un uno:  en un circuito eléctrico, el circuito está cerrado cuando está presente la afirmación de V.

Falso

El valor falso F; si se emplea notación numérica se expresa con un cero: 0; en un circuito eléctrico, el circuito está abierto.

Negación

La negación es un operador que se ejecuta, sobre un único valor de verdad, devolviendo el valor contradictorio de la proposición considerada.

Conjunción

La conjunción es un operador, que actúa sobre dos valores de verdad, típicamente los valores de verdad de dos proposiciones, devolviendo el valor de verdad verdadero cuando ambas proposiciones son verdaderas, y falso en cualquier otro caso. Es decir, es verdadera cuando ambas son verdaderas.

En términos más simples, será verdadera cuando las dos proposiciones son verdaderas.

Disyunción

La disyunción es un operador lógico que actúa sobre dos valores de verdad, típicamente los valores de verdad de dos proposiciones, devolviendo el valor de verdad verdadero cuando una de las proposiciones es verdadera, o cuando ambas lo son, y falso cuando ambas son falsas.

En términos más simples, será verdadera cuando por lo menos una de las proposiciones es verdadera de lo contrario será falsa.

Condicionante

El condicionante es un operador que actúa sobre dos valores de verdad, típicamente los valores de verdad de dos proposiciones, devolviendo el valor de falso solo cuando la primera proposición es verdadera y la segunda falsa, y verdadero en cualquier otro caso.

Bicondicional

La bicondicional es una operación binaria lógica que asigna el valor verdadero cuando las dos variables son iguales y el valor falso cuando son diferentes.

Conectores lógicos

Las proposiciones genéricas se denotan con las letras p$\mathrm{<br>}$, q$\mathrm{<br>}$, r$\mathrm{<br>}$, etc. Estas proposiciones son simples y con estas se puede operar para generar otras proposiciones, ya sea simples o compuestas, y según sean las operaciones se utilizan ciertos símbolos, llamados conectores o conectivos lógicos.

Conectivo	Operación asociada	Significado
¬$\neg$	Negación	no p$�$ o no es cierto que p$�$
∨$\vee$	Conjunción o producto lógico	p$�$ y q$�$
∧$\wedge$	Disyunción o suma lógica	p$�$ o q$�$ en sentido excluyente
→$\to$	Implicación	p$�$ implica q$�$ o si p$�$, entonces q$�$
↔$\leftrightarrow$	Doble implicación	p$�$ si y sólo si q$�$

Operaciones proposicionales

Las operaciones entre proposiciones se definen como: dadas una o dos proposiciones, cuyos valores de verdad se conocen, se trata de caracterizar la proposicón resultante a traves de su valor de verdad. Se supone que en la elección de estos valores se tiene en cuenta el buen sentido

La geometría plana

La geometría plana analiza elementos como unidimensionales como la recta, la semirrecta y el segmento. De igual modo, forman parte de este campo de estudios los ángulos y los polígonos.

Esta rama de geometría implica muchas veces la simplificación del mundo que nos rodea en un plano, de manera que no pueden estudiarse todas las características de los objetos. Por ejemplo, no se podría analizar todas las dimensiones de una caja, sino cada una de sus caras que son cuadriláteros.

La geometría plana tiene sus orígenes en la antigüedad, siendo su principal antecedente la obra Los Elementos del matemático griego Euclides y que data del siglo IV A.C. Este es considerado como uno de los textos más influyentes de la historia y recopila nociones básicas de elementos como rectas y polígonos, e incluso podemos encontrar el famoso teorema de Pitágoras.

Recta: Es un elemento unidimensional constituido por una serie infinita de puntos que van a una sola dirección, es decir, no presenta curvas.

Semirrecta: Al igual que la recta, es un elemento unidimensional que consiste en una secuencia de puntos, pero no es indefinida, sino que tiene un origen y se prolonga al infinito. Puede definirse también como la porción de una recta definida a partir de un punto de corte.

Segmento: Es un elemento unidimensional constituido puntos que van en una sola dirección, pero , a diferencia de la semirrecta, está acotado por un punto de origen y un final.

Ángulo: Es el arco que se forma a partir del cruce u origen de dos elementos bidimensionales, ya sean rectas, semirrectas o segmentos.

Polígono: Es una figura bidimensional formada por una serie finita de segmentos no colineales (no forman parte de la misma recta), de manera que forman un espacio cerrados. Algunos ejemplos son los cuadrados, los rectángulos, los rombos, los triángulos o los octógonos. Los polígonos pueden clasificarse en:

Regulares: Cuando todos sus lados y ángulos interiores tienen la misma medida.

Irregulares: Cuando no todos sus lados y ángulos interiores son idénticos.

Circunferencia: Es una figura geométrica plana y cerrada que se caracteriza porque todos los puntos que la constituyen se ubican a la misma distancia del centro. Dicha distancia constante se llama radio. También se define a la circunferencia como el perímetro del círculo.

 Polígonos

Un polígono es una figura plana cerrada que está formada por tres o más segmentos de recta que se unen en sus puntos extremos. Los segmentos de recta que forman un polígono solo se intersectan en sus puntos extremos. Los polígonos se nombran de acuerdo al número de lados que están formados.

 

Triángulo: polígono de 3 lados                                   Cuádrilatero: polígono de 4 lados

Pentagono: polígono de 5 lados                              Hexágono: polígono de 6 lados

Heptágono: polígono de 7 lados                              Octágono: polígono de 8 lados

Nonágono: polígono de 9 lados                               Decágono: polígono de 10 lados

Dodecágono: polígono de 12 lados                          n - ágono: polígono de n lados

 

Círculos

El círculo es una figura plana que consiste de todos los puntos que están sobre una curva cerrada y de los puntos interiores de ella, en la cual cada punto sobre la curva tiene la misma distancia al centro del círculo.El radio de un círculo es la distancia entre el centro y cualquier punto de la curva y tiene longitud r.El diámetro de un círculo es la distancia entre dos puntos cualesquiera de la curva cerrada y que pasapor el centro y tiene longitud d = 2r y divide a un círculo en dos partes iguales.

La Circunferencia es la línea curva cerrada y plana cuyos puntos están a la misma distancia (radio) de un punto (centro). El centro no es parte de la circunferencia.

El área de un círculo, es la medida de la superficie limitada por la circunferencia del círculo dado.

En la siguiente aplicación mueve los deslizadores y luego:

Compara las superficies del polígono inscrito en la circunferencia y la del círculo delimitado por la misma.

Aumenta el número de lados y cambia la longitud del radio ¿Qué harías para que la superficie del polígono fuese lo más parecida posible a la del círculo?

Activa las casillas "Datos del polígono" y "Radio". Repite las actividades uno y dos. Comprueba que la respuesta que has dado en la actividad dos es la correcta.

Activa las casillas "Área del polígono" y "Área del círculo". Comprueba si la respuesta dada en la actividad dos es acorde con los datos de las áreas.

 

Trigonometría

La trigonometría es la parte de la matemática que se encarga de estudiar y medir los triángulos, las relaciones entre sus ángulos y lados, y sus funciones trigonométricas deseno, coseno, tangente, cotangente, secante y cosecante.

Esta rama matemática se relaciona, directa o indirectamente, con otras áreas científicas, y se aplica atodo aquello que requiera de medidas de precisión, como la geometría espacial y la astronomía para la medición de las distancias entre estrellas respecto a otros puntos geográficos.

El estudio de la trigonometría existe desde hace más de tres mil años. En Babilonia y Egipto se tomaban en cuenta las medidas de los ángulos de los triángulos para construir pirámides.

¿Cuál es la importancia de la trigonometría?

La aplicación  de las funciones trigonométricas en la física, astronomía, telecomunicaciones, náutica, ingeniería, cartografía, entre otros ámbitos, es lo que las dota de relevancia, pues permiten calcular distancias con precisión sin tener que, necesariamente, recorrerlas.

abiendo esto, la importancia de la trigonometría radica en las diversas aplicaciones que tiene para, por ejemplo:

Calcular la distancia entre dos puntos, de los cuales uno, o incluso ambos, son inaccesibles.

Calcular de forma precisa distancias y ángulos de inclinación, siendo de gran utilidad para la ingeniería civil.

Calcular la altura de un punto en pie que puede ser, también, inaccesible.

¿Cuáles son las unidades de medida en trigonometría?

Cuando se estudia la medida de los ángulos, así como su cálculo, la trigonometría se vale de las siguientes unidades:Radián: unidad angular básica en trigonometría que indica la relación que existe entre el ángulo que se forma a partir del radio de una circunferencia y un arco que tenga la misma longitud. Una circunferencia completa está conformada por dos radianes.

Grado sexagesimal: unidad angular que divide una circunferencia en 360 grados, considerando que cada ángulo recto posee 90 grados y si se divide la circunferencia a cuatro partes iguales, la suma de cada

ángulo dará un total de 360. Se suele utilizar en el campo práctico de ramas como la ingeniería, arquitectura o la física.

Grado centesimal: unidad angular que divide una circunferencia en 400 grados centesimales.

Mil angular: unidad que divide la circunferencia en 6.400 unidades.

¿Cuáles son las funciones trigonométricas?

Se entiende por funciones trigonométricas a la relación métrica entre los lados de un triángulo rectángulo. A partir de un triángulo que presente un ángulo recto de 90 grados se pueden determinar tres elementos fundamentales:

 

Ángulos: área del plano que se encuentra entre dos semirrectas con origen común. Se trata de la amplitud del arco de una circunferencia, centrada en el vértice y delimitada por sus lados.

Catetos: resto de lados que conforman un triángulo. Se pueden clasificar en cateto opuesto (que se encuentra del lado opuesto o en frente del ángulo estudiado) y el adyacente (que se encuentra junto al ángulo analizado).

Hipotenusa: lado de mayor longitud de un triángulo y está opuesto al ángulo recto.

Entendidos estos tres conceptos fundamentales, las funciones trigonométricas son:

seno: razón que existe entre el cateto opuesto del ángulo de estudio y la hipotenusa.

Coseno: división del cateto adyacente del ángulo analizado entre la hipotenusa del triángulo.

Tangente: razón que existe entre el lado opuesto y el cateto adyacente del triángulo. Se expresa como la división del seno entre el coseno.

Secante: razón recíproca del coseno que consiste en la relación entre la longitud de la hipotenusa y la longitud del cateto adyacente.

Cosecante: razón recíproca del seno que consiste en la relación entre la longitud de la hipotenusa y la longitud del cateto opuesto.

Cotangente: razón recíproca de la tangente que consiste en la relación entre la longitud del cateto adyacente y la del opuesto.

 FUNCIONES LINEALES

Una función lineal es una función polinómica de primer grado. Es decir, tiene la siguiente forma

Definimos función lineal y explicamos algunos conceptos: pendiente, ordenada, gráfica, punto de corte con los ejes, intersección de dos funciones, rectas paralelas y perpendiculares. Finalmente, resolvemos problemas de aplicación. Matemáticas. Secundaria.

siendo m≠0.

m es la pendiente de la función

n es la ordenada (en el origen) de la función

La gráfica de una función lineal es siempre una recta.

 Ejemplo:

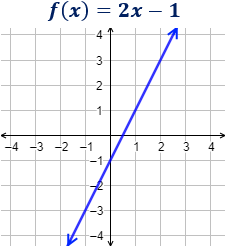
Definimos función lineal y explicamos algunos conceptos: pendiente, ordenada, gráfica, punto de corte con los ejes, intersección de dos funciones, rectas paralelas y perpendiculares. Finalmente, resolvemos problemas de aplicación. Matemáticas.

Secundaria.La pendiente de la recta es m = 2 y la ordenada es n = -1.

Geométricamente, cuanto mayor es la pendiente, más inclinada es la recta. Es decir, más rápido crece la función.Si la pendiente es positiva, la función es creciente.

Si la pendiente es negativa, la función es decreciente.

Puntos de corte

Una función lineal siempre corta al eje Y en un punto. También, corta al eje X en un punto.

El punto de corte con el eje Y es el punto de la recta que tiene la primera coordenada igual a 0:

El punto de corte con el eje X es el punto de la recta que tiene 0 en la segunda coordenada. Se calcula igualando a 0 la función y resolviendo la ecuación obtenida.

Ejemplo:

Calculamos los puntos de corte de la función del ejemplo anterior,

Corte con el eje Y:

Es el punto

Observad que la segunda coordenada es la ordenada. Corte con el eje X:

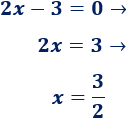
Es el punto

La pendiente

La pendiente es la inclinación de la recta con respecto al eje de abscisas.

Se denota con la letra m.

Si m > 0 la función es creciente y ángulo que forma la recta con la parte positiva del eje OX es agudo.

Si m < 0 la función es decreciente y ángulo que forma la recta con la parte positiva del eje OX es obtuso.

La pendiente de una recta es la tangente del ángulo que forma la recta con la dirección positiva del eje de abscisas.

Cálculo de la pendiente

Pendiente dado el ángulo

Pendiente dado el vector director de la recta

Pendiente dados dos puntos

Pendiente dada la ecuación de la recta.

ECUACIÓN GENERAL DE LA RECTA

La ecuación general de una recta es una expresión de la forma Ax+By+C=0, donde A, B y C son números reales.

La pendiente de la recta es el coeficiente de la x una vez puesta en forma explícita (es decir, despejada y):

By = -Ax-C   ->    -> la pendiente es: m = -A/B

 

 1. La ecuación general de una recta es 2x-3y+6=0. Calcula la pendiente de la recta.

 2. Calcula el valor de k para que la ecuación de la recta kx+3y-9=0 tenga por pendiente 

m=-1.

 Ecuaciones de primer grado con una incógnita. Procedimiento para resolver una ecuación de 1r grado: 

• Quitar denominadores: multiplicando ambas partes de la ecuación por el mínimo común múltiplo de los denominadores. (Propiedad 2)

• Quitar paréntesis. (Propiedad distributiva) 

• Transposición de términos. Conseguir una ecuación de la forma a ⋅ x = b . (Propiedad 1). 

• Despejar la incógnita. (Propiedad 2).

 • Comprobar la solución.

 Una ecuación es una igualdad matemática entre dos expresiones, denominadas miembros y separadas por el signo igual, en las que aparecen elementos conocidos y datos desconocidos o incógnitas, relacionados mediante operaciones matemáticas. Los valores conocidos pueden ser números, coeficientes o constantes, también variables o incluso objetos complejos como funciones o vectores; los elementos desconocidos pueden ser establecidos mediante otras ecuaciones de un sistema o algún otro procedimiento de resolución de ecuaciones.nota 1​Las incógnitas, representadas generalmente por letras, constituyen los valores que se pretende hallar (en ecuaciones complejas en lugar de valores numéricos podría tratarse de elementos de un cierto conjunto abstracto, como sucede en las ecuaciones diferenciales). Por ejemplo, en la ecuación algebraica siguiente:

 

la variable  representa la incógnita, mientras que el coeficiente 3 y los números 1 y 9 son constantes conocidas. La igualdad planteada por una ecuación será cierta o falsa dependiendo de los valores numéricos que tomen las incógnitas; se puede afirmar entonces que una ecuación es una igualdad condicional, en la que solo ciertos valores de las variables (incógnitas) la hacen cierta.

Se llama solución de una ecuación a cualquier valor individual de dichas variables que la satisface. Para el caso dado, la solución es:

 Inecuaciones

Las inecuaciones son expresiones algebraicas que se relacionan a partir de desigualdades. Dichas relaciones se expresan mediante los signos > (mayor que), < (menor que), ≥ (mayor o igual que) o ≤ (menor o igual que). Las inecuaciones se conforman por valores conocidos y desconocidos. Estos últimos son llamados incógnitas.

Tipos de inecuaciones

La clasificación común de las inecuaciones se da de acuerdo a dos criterios principales: el número de incógnitas y la potencia de la incógnita.

Inecuaciones según el número de incógnitas

Inecuaciones de una incógnita.

Inecuaciones de dos incógnitas.

Inecuaciones de tres incógnitas.

Inecuaciones según la potencia de la incógnita

Lineal o de primer grado. Estas se presentan cuando el mayor exponente de la incógnita es uno.

¿Qué se debe hacer para resolver una inecuación?

Para resolver una inecuación se debe despejar la incógnita o las incógnitas. Con el fin de lograrlo, deberás tener en cuenta los siguientes pasos:

 

Agrupa los términos semejantes. Pasa las incógnitas al lado izquierdo y las constantes al lado derecho.

Suma y resta u opera las términos semejantes.

Determina el valor de la incógnita. Despéjala.

Ten en cuenta que los valores deberán satisfacer la inecuación que se ha formulado.

Ejemplo: resolución de inecuación lineal

Sistema de ecuaciones algebraicas

En matemáticas, un sistema de ecuaciones algebraicas es un conjunto de ecuaciones con más de una incógnita que conforman un problema matemático que consiste en encontrar los valores de las incógnitas que satisfacen dichas operaciones.

 

En un sistema de ecuaciones algebraicas, las incógnitas son valores numéricos menores a la constante (o más generalmente elementos de un cuerpo sobre el que se plantean las ecuaciones), mientras que en una ecuación diferencial las incógnitas son funciones o distribuciones de un cierto conjunto definido de antemano. Una solución de dicho sistema es por tanto, un valor o una función que substituida en las ecuaciones del sistema hace que éstas se cumplan automáticamente sin que se llegue a una contradicción. En otras palabras el valor que reemplazamos en las incógnitas debe hacer cumplir la igualdad del sistema.

 las incógnitas se suelen representar utilizando las últimas letras del alfabeto latino, o si son demasiadas, con subíndices.

Sistema general

La forma genérica de un sistema de m\, ecuaciones algebraicas y n\, incógnitas es la siguiente:

son funciones de las incógnitas. La solución, perteneciente al espacio euclídeo , será tal que el resultado de evaluar cualquier expresión  con los valores de dicha solución, verifique la ecuación.

Representación gráfica

Los sistemas de 2 o 3 incógnitas reales admiten representaciones gráficas cuando las funciones  en (1) son continuas a tramos. En cada ecuación se representa como una curva o una superficie curva. La existencia de soluciones en ese caso puede deducirse a partir de la existencia de intersecciones comunes a dichas curvas o superficies curvas. Los sistemas de 2 o 3 incógnitas reales admiten representaciones gráficas cuando las funciones  en (1) son continuas a tramos. En cada ecuación se representa como una curva o una superficie curva. La existencia de soluciones en ese caso puede deducirse a partir de la existencia de intersecciones comunes a dichas curvas o superficies curvas.

Una ecuación lineal con dos incógnitas es una igualdad del tipo ax+by=c, donde a, b, y c son números, y «x» e «y» son las incógnitas.

Una solución es todo par de números que cumple la ecuación.

Los sistemas de ecuaciones lineales los podemos clasificar según su número de soluciones:

• Compatible determinado: Tiene una única solución, la representación son dos rectas que se cortan en un punto.
• Compatible indeterminado: Tiene infinitas soluciones, la representación son dos rectas que coinciden.
• Incompatible: No tiene solución, la representación son dos rectas paralelas.

 Existen diferentes métodos de resolución:

• Sustitución.
•  Reducción.
•  Igualación.

En esta ocasión vamos a resolver un sistema de dos ecuaciones lineales con dos incógnitas. Por ejemplo:

Sistema de ecuaciones: método de sustitución

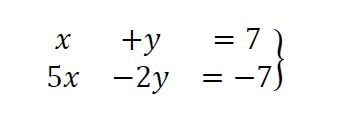
A través del método de sustitución lo que debemos hacer es despejar una de las incógnitas en una de las ecuaciones y sustituir su valor en la siguiente. Lo veremos con más detalle en el siguiente ejemplo:

Lo primero que hacemos es despejamos una de las incógnitas en la primera ecuación.

x+y=7
x= 7-y

Posteriormente, sustituimos en la segunda ecuación el valor correspondiente de la «x».

5x-2y=-7
5.(7-y)-2y=-7

Ahora, despejamos la «y».

35-5y-2y=-7
35-7y=-7
-7y=-7-35
-7y=-42
y=-42/-7=6

y=6

Por último, utilizamos el valor de «y» para hallar el valor de «x».

x= 7-y

x=7-6=1

x=1

La solución de nuestro sistema es x=1 e y =6.

Sistema de ecuaciones: método de reducción

Con el método de reducción lo que hacemos es combinar, sumando o restando, nuestras ecuaciones para que desaparezca una de nuestras incógnitas.

Los pasos a seguir son los siguientes:

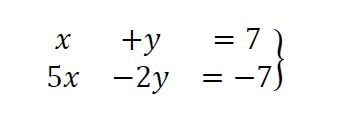
En primer lugar, necesitamos preparar las dos ecuaciones, si es necesario, multiplicándolas por los números que convenga.

En este caso, queremos reducir la «y» de nuestro sistema, por tanto, multiplicamos la primera ecuación por 2.

2(x+y=7)
5x-2y=-7

Así, el sistema se queda:

Si nos fijamos, sumando las ecuaciones la y nos desaparece.

Y nos quedaría:

7x=7
x=7/7=1
x=1

Por último, sustituimos el valor que hemos calculado despejando la otra incógnita en una de las ecuaciones iniciales.

y= 7-x

y=7-1=6

y=6

La solución de nuestro sistema es x=1 e y =6.

Sistema de ecuaciones: método de igualación

El método de igualación consiste en despejar la misma incógnita en las dos ecuaciones y después igualar los resultados.

Los pasos a seguir son los siguientes:

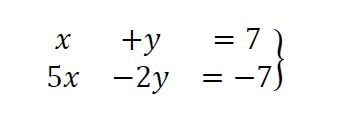
En primer lugar, elegimos la incógnita que deseamos despejar. En este caso, empezaré por la «x» y despejo la misma en ambas ecuaciones.

x+y=7; x=7-y

5x-2y=-7; 5x=2y-7; x=(2y-7)/5

Una vez hemos despejado, igualamos:

7-y=(2y-7)/5
5(7-y=(2y-7)/5)
35-5y=2y-7
42=7y
y=42/7=6

y=6

Por último, sustituimos el valor que hemos calculado despejando la otra incógnita en una de las ecuaciones iniciales.

x=7-y
x=7-6=1

x=1

La solución de nuestro sistema es x=1 e y =6.

¿Qué son las matrices?

Las matrices son un conjunto bidimensional de números o símbolos distribuidos de forma rectangular, en líneas verticales y horizontales, de manera que sus elementos se organizan en filas y columnas. Sirven para describir sistemas de ecuaciones lineales o diferenciales, así como para representar una aplicación lineal.

 Toda matriz se representa por medio de una letra mayúscula, y sus elementos se reúnen entre dos paréntesis o corchetes, en letra minúscula. A su vez, tienen doble superíndice: el primero hace referencia a la fila y el segundo a la columna a la que pertenece.

 Esta expresión matemática puede sumarse, multiplicarse y descomponerse, por lo que su uso es común en el álgebra lineal. 

 Esta expresión matemática puede sumarse, multiplicarse y descomponerse, por lo que su uso es común en el álgebra lineal. 

Algunos de los conceptos necesarios para completar la definición y el análisis de las matrices son:

 

Elementos: son los números que conforman la matriz.

Dimensión: se trata del resultado del número de filas por el número de columnas. Se designa la m al número de filas y n al número de columnas.

Anillos: se trata de un término propio del álgebra y hace referencia al sistema formado por un conjunto de operaciones internas que responden a una serie de propiedades. Las matrices se entienden como elementos de un anillo.

Función: se trata de una regla de correspondencia entre dos conjuntos en el que un elemento del primer conjunto se corresponde, exclusivamente, con un solo elemento el segundo conjunto.

¿Qué tipos de matrices existen?

Una matriz puede ser:

Rectangular: tiene diferentes números de filas y columnas.

Fila: una matriz rectangular, pero con una sola fila.

Columna: una matriz rectangular, pero con una sola columna.

Nula: matriz cuyos elementos son iguales a cero.

Cuadrada de orden n: matriz que tiene el mismo número de filas que de columnas. En este tipo de matrices, la dimensión se llama orden, y su valor coincide con el número de filas y columnas.

Diagonal: es un tipo de matriz cuadrada en la que los elementos que no se encuentran en la diagonal principal son iguales a cero.

Escalar: es una matriz diagonal en la que todos los elementos presentes en la diagonal principal son iguales.

Identidad: se trata de una matriz escalar en la que los elementos de la diagonal principal son iguales a uno, mientras que el resto de los elementos son iguales a cero.

Opuesta: es opuesta a otra cuyos elementos tienen un signo contrario a la matriz principal. Es decir, la matriz opuesta a A se denomina -A y todos los elementos del conjunto son contrarios a los elementos de la matriz A.

Traspuesta: se trata de la matriz que se obtiene al convertir las filas en columnas. Se utiliza el superíndice t para representarla y su dimensión es n x m.

Triangular superior: se trata de una matriz cuadrada en la que al menos uno de los términos que está por encima de la diagonal principal es distinto a cero, y todos los que están situados por debajo a ella son iguales a cero.

Triangular inferior: a diferencia del tipo anterior, en este tipo de matriz al menos uno de los elementos que están debajo de la diagonal principal son diferentes a cero y todos los que están por encima de ella son iguales a cero.